[전자기학 w/MATLAB] quiver plot - 구면위의 벡터장

아 근데 전문적인 정리 글 아니고요 걍 학부생이 정리한 글인데 그래도 우리 후배님들한텐 꽤 쓸만할거에요

part 1 _ Theory

z방향으로 uniformly magnetized된 ball의 magnetic field를 계산해보자.

먼저 bound currents 를 계산해준다. (notation 천정각 $\theta$)

 

volume current 는 0이고, bound surface current  $K_b$ 는

표면에 전하 $\sigma$가 덕지덕지 붙은 채 $z$축 각속도 $\omega$ 로 회전하는

sphere로 생각('identify')할 수 있다.

 

이 identification은 물론 당장 vector potential을 구하는데에는 불필요하다.

하지만 Magnetization에 의한 B-field와 current에 의한 그것이 완전히 identify되는 것은 

개념적으로 몹시 편리하므로 교과서에서도 이 점을 짚고 넘어가고 있다.

(물론 $\sigma$ 가 그래서 얼마인지를 물으면,, 할말이 없다.

거기에 이 비유를 더 밀고나가서 여기서 E-field가 있다고 주장한다면 더욱 할 말이 없다.)

 

part2 _ Lab1 

Misson : $K_b$ 를 visualize(시각화) 해보자

참고로 저는 matlab을 오늘 처음 써봅니다..... 더 좋은 방법이 있으면 comment로 알려주시면 

바로 업데이트 하도록 하겠습니다!!

 

첫번째는 unit sphere를 구성하는 점들의 좌표를 얻어오는 일이 되시겠다.

그래야 그 좌표에 vector field 화살표들을 찍을 수 있을 테니까.

[X, Y, Z] = sphere;

 

아래는 sphere 관련 mathworks의 reference이다. 짧으니 읽고오길 추천!

https://www.mathworks.com/help/matlab/ref/sphere.html

Create sphere - MATLAB sphere

일단 [X,Y,Z] 가 무슨 문법인지는 차치하고서라도,

X, Y, Z 에 뭐가 들어있는지 보면 대강 matlab이 sphere를 어떻게 다루는지를 볼 수 있겠다.

 

그냥 매트랩 인강이나 좀 알아볼깤ㅋㅋ 이렇게 배우는게 효율이 나오낰ㅋㅋ

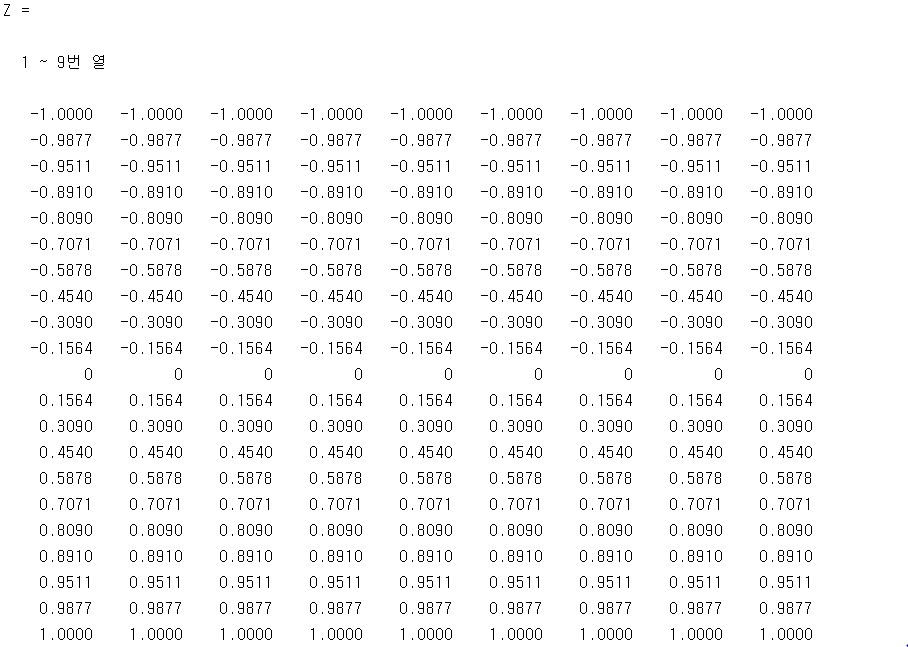
아직 그래도 첫날이니까 집념으로 분석해보면,, 그냥 [-1, 1] 구간을 21등분 한 값들이 나온다.

21*21 matrix에서 각 row 가 같은 Z값을 갖는 것을 알 수 있다.

 

X를 보면 좀 심란하다.

먼저 저 Z를 보니까 21등분의 가운데인 10층.. 에서 X좌표들을 봐야겠다는 생각이 들었다.

응 unit circle의 x좌표들이다. 

대강 [X,Y,Z] 가 각각 어떻게 구 표면의 좌표들을 나타내는지 감이 온다.

 

exercise 1.1.1

Q_ unit sphere에서 x, y, z 값이 모두 양인 부분만을 그려라.

 

하여간 이제 우리의 목표는 

$K_b = \sigma R\omega sin(\theta)\hat{\phi}$ 를 그리는 것이다...

후.... 구면좌표계네.. 좌표변환을 해주는

cart2sph 를 쓰는게 좋겠다. (실제로 나는 이 함수의 존재를 몰라서.. 아래와 같은 코드를 썼다.ㅋㅋㅋㅋ)

 

R = sqrt(X.^2 + Y.^2 + Z.^2);
THETA = acos(Z./R);
PHI = atan(Y./X);

이 블로그에서 PHI는 항상 $0$에서 $2pi$ 까지이다.

그리고 저 atan 함수는 range가 하여간 2pi까지 가지는 않는다. 

따라서 저 간단한 변환은 먹히지 않고,, cart2sph를 써보자.

[az,el,r] = cart2sph(X,Y,Z);

 

az, el, r이 각각 azimuthal angle, elevation, radius인가보다.

각 angle의 range는 저렇게 준다.

 

그리고 바로 quiver3를 써서 $\hat{\phi}$ 를 그려봤다.

quiver3가 3d 화살표를 그리는 함수인데, reference를 보고 오자.

https://www.mathworks.com/help/matlab/ref/quiver3.html

3-D quiver or vector plot - MATLAB quiver3

결국 X,Y,Z 위치에 (U,V,W)방향의 화살표를 그린다는건데,,,

화살표가 너무 길거나 짧게 그려진다면 scaling은 W다음에 바로 주면 된다.

일단은 기본적으로는 unit length 화살표를 그리는 것 같다.

아래 코드에서 Z.*0 의 .* 는 componentwise 곱을 뜻한다. (matrix의 각 대응되는 위치의 값을 곱한다는 뜻)

 21by21 zero matrix를 뭐 zeros(size(Z)) 인가?? 이런식으로 만들수도 있었겠지만 그냥 귀찮아서 저리 했다.

quiver3(X, Y, Z, -sin(az), cos(az), Z.*0);
axis equal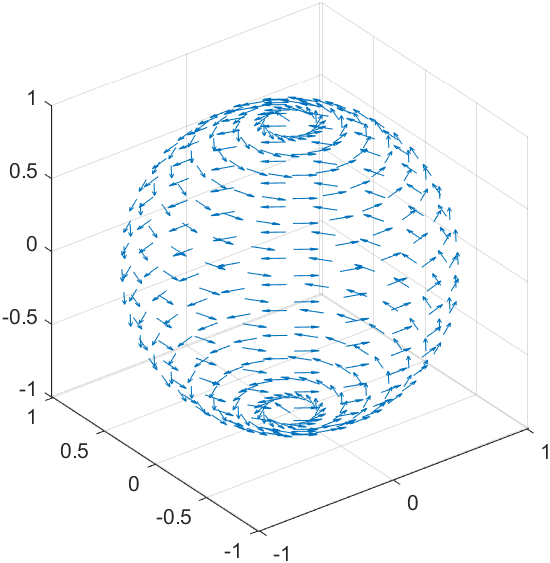

이제 size를 $\sigma R\omega$ 무시하고 $sin(\theta)$만 가지고 그려주면,

[X, Y, Z] = sphere;
[az,el,r] = cart2sph(X,Y,Z);
quiver3(X, Y, Z, -sin(az), cos(az), Z.*0, sin(pi/2 - el));
axis equal

쪼께.. 보기가 나쁜것 같지만 눈 크게 뜨고 보면 맞게 그려놨다.

아래 그림은 구도 함께 그려줬고, 구랑 같이 그리니까 화살표가 잘 안보여서 길이랑 굵기랑 색깔을 다 바꿔줬다.

아래 코드에서 hold on; 은 현재 그림을 지우지 말고 계속 그 위에 그리게 냅두라는 뜻이다.

또 parameter list가 길어져서 줄바꿈을 했는데 줄바꿈 하려면 ... 을 꼭 붙여줘야 하더라... 

[X, Y, Z] = sphere;
sphere;
hold on;
[az,el,r] = cart2sph(X,Y,Z);
quiver3(X, Y, Z, -sin(pi/2 - el).*sin(az), sin(pi/2 - el).*cos(az), Z.*0, 2, ...
    'Color','r', 'LineWidth', 1.0);
axis equal

하,, 이제 vector potential을 계산하러 가자..